多孔(kong)孔闆流(liu)量計 是(shi)一種節(jie)流式流(liu)量計，在(zai)圓形闆(pan)片上布(bu)置多個(ge)介質流(liu)通孔．對(dui)按照特(te)定方式(shi)設計的(de)多孔孔(kong)闆局部(bu)壓力損(sun)失系數(shu)🏃‍♀️ξ和節流(liu)特性的(de)主效應(ying)因素進(jin)行分析(xi)，拟合出(chu)局部壓(ya)力損失(shi)系數ξ與(yu)等效直(zhi)徑比β之(zhi)間的關(guan)系式，并(bing)且得出(chu)等效直(zhi)徑比β是(shi)影響多(duo)孔孔闆(pan)🔅節流效(xiao)應的主(zhu)效應因(yin)素🧡．将A＋FlowTeK的(de)多孔孔(kong)🎯闆流量(liang)計同👌傳(chuan)統節流(liu)裝🔴置進(jin)行比較(jiao)，得出多(duo)孔孔闆(pan)流量計(ji)具有精(jing)度高、壓(ya)損小、需(xu)要前後(hou)直管段(duan)短等優(you)點．利用(yong)孔❤️分布(bu)、孔闆厚(hou)度以及(ji)擾動對(dui)多孔孔(kong)闆的流(liu)出系數(shu)Cd的影響(xiang)．
　　介質經(jing)過多孔(kong)節流件(jian)後形成(cheng)多股受(shou)限型射(she)流，由于(yu)多股射(she)流之間(jian)的卷吸(xi)和摻混(hun)，增加了(le)流場的(de)複雜性(xing)🈲．Taylor在1949年提(ti)出了射(she)流卷🥵吸(xi)假說，1986年(nian)Tumer對這個(ge)假說的(de)發展進(jin)🏒行了詳(xiang)細說明(ming)．系統地(di)研究了(le)射流入(ru)射間距(ju)對雙股(gu)射流彙(hui)聚區和(he)聯合區(qu)流動結(jie)構的影(ying)響；利用(yong)PIV技術在(zai)入射速(su)度不🛀同(tong)的情況(kuang)下🥵對雙(shuang)股平行(hang)射流的(de)卷吸效(xiao)應、湍流(liu)強度、速(su)度剖面(mian)以及雷(lei)✍️諾應力(li)進行了(le)⭕研究．利(li)用PLIF技術(shu)對平行(hang)雙股射(she)流流場(chang)中的混(hun)合區進(jin)行測量(liang)．長期以(yi)來研究(jiu)人員‼️分(fen)别從理(li)論分析(xi)、實驗測(ce)量和數(shu)值模拟(ni)方面對(dui)多股射(she)流進行(hang)了大量(liang)的工作(zuo)📱，對流場(chang)中的一(yi)些流動(dong)💯特性和(he)流動機(ji)理取得(de)了豐富(fu)的成果(guo)．利用多(duo)股射流(liu)理論和(he)實驗相(xiang)結合的(de)方法對(dui)多孔孔(kong)闆計量(liang)精度的(de)影響因(yin)素．
1結構(gou)與工作(zuo)原理
　　多(duo)孔孔闆(pan)流量計(ji)的簡化(hua)結構如(ru)圖1所示(shi)，即在封(feng)閉的管(guan)🌍道内同(tong)軸安裝(zhuang)多孔孔(kong)闆，來流(liu)方向如(ru)圖1（a）中箭(jian)🌐頭所示(shi)，采用壁(bi)✨面取壓(ya)方式．

不可壓(ya)縮流體(ti)的體積(ji)流量計(ji)算公式(shi)爲

　　式中(zhong)：qV爲體積(ji)流量，m3/s；Δp爲(wei)差壓，爲(wei)影響流(liu)出系數(shu)Cd的關鍵(jian)因素，Pa；Cd爲(wei)⭕流🚶‍♀️出系(xi)數，無量(liang)綱，該參(can)數是從(cong)實驗中(zhong)獲得；ρ爲(wei)流體密(mi)度，kg/m3；β爲等(deng)效直徑(jing)比；ds爲節(jie)流孔的(de)等效直(zhi)徑．
2影響(xiang)計量精(jing)度的因(yin)素分析(xi)
　　圖2爲管(guan)徑100,mm、β=0.6的多(duo)孔孔闆(pan)流量計(ji)在雷諾(nuo)數爲52×10的(de)條件下(xia)的内🧑🏾‍🤝‍🧑🏼部(bu)流場的(de)速度矢(shi)量圖，在(zai)上下遊(you)取壓口(kou)處♍取截(jie)面Ⅰ和Ⅱ，根(gen)據不可(ke)壓縮流(liu)體的伯(bo)努利方(fang)程

　　式中(zhong)：p1和p2分别(bie)爲截面(mian)Ⅰ和Ⅱ處的(de)靜壓力(li)；v1和v2分别(bie)爲截面(mian)💰Ⅰ和Ⅱ處的(de)平均速(su)度；ξ爲局(ju)部壓損(sun)系數；表(biao)示截面(mian)Ⅰ和Ⅱ處的(de)動能變(bian)化量；表(biao)示内能(neng)損失，與(yu)多孔孔(kong)闆結構(gou)相關．根(gen)據動能(neng)
第2表達(da)式得

式(shi)中：ω爲渦(wo)量；v爲速(su)度矢量(liang)；r爲觀測(ce)點與旋(xuan)轉中心(xin)之間的(de)矢徑☀️．
　　各(ge)流量點(dian)下流出(chu)系數Cd的(de)線性度(du)是衡量(liang)多孔孔(kong)闆計量(liang)☀️精度的(de)評價指(zhi)标，由式(shi)(2)、式(5)、式(6)可(ke)知，流出(chu)系數Cd主(zhu)要受🌂渦(wo)量影響(xiang)．

　　介質(zhi)經過多(duo)孔孔闆(pan)後形成(cheng)多股受(shou)限型射(she)流，射流(liu)自⛱️孔口(kou)出射後(hou)與周圍(wei)靜止流(liu)體間形(xing)成速度(du)不連續(xu)的⛹🏻‍♀️間斷(duan)面，間斷(duan)面失穩(wen)而産生(sheng)漩渦．漩(xuan)渦卷吸(xi)周圍流(liu)體進入(ru)到射流(liu)，同時不(bu)斷移動(dong)、變形、分(fen)裂産生(sheng)👄紊動，其(qi)影響逐(zhu)漸向内(nei)外發展(zhan)形成内(nei)外兩個(ge)自由紊(wen)動的剪(jian)切層．自(zi)由剪切(qie)層中的(de)漩渦通(tong)過分裂(lie)、變形、卷(juan)吸和合(he)并🈲等物(wu)理過程(cheng)，除了形(xing)成大量(liang)的随機(ji)🧑🏽‍🤝‍🧑🏻運動小(xiao)尺度紊(wen)動渦體(ti)外😍，還存(cun)在一部(bu)分有序(xu)的大尺(chi)度渦結(jie)構．大尺(chi)度🔞渦的(de)拟序結(jie)構由縱(zong)向渦和(he)展向渦(wo)組成，其(qi)中展向(xiang)渦結構(gou)對剪切(qie)層的發(fa)展控制(zhi)💃起主要(yao)作用，對(dui)紊流的(de)産生、能(neng)量的傳(chuan)遞🏃🏻、動量(liang)輸運和(he)紊動摻(chan)混等産(chan)生直接(jie)影響[11-26]，因(yin)此，大尺(chi)度的展(zhan)向渦結(jie)㊙️構是影(ying)響多孔(kong)孔闆流(liu)量計㊙️計(ji)量性能(neng)的關鍵(jian)因素．
　　大(da)尺度渦(wo)對周圍(wei)流體有(you)強烈的(de)卷吸作(zuo)用，使周(zhou)圍⛷️流體(ti)随射流(liu)而運動(dong)，增加了(le)射流的(de)總質量(liang)．卷吸量(liang)是反映(ying)射流卷(juan)吸作用(yong)強弱的(de)标準，其(qi)大小與(yu)剪切層(ceng)中大🆚尺(chi)度渦的(de)發展演(yan)化過程(cheng)及強度(du)相關．在(zai)管壁的(de)約束下(xia)，介質進(jin)💃入多孔(kong)孔闆後(hou)形成🔱的(de)射流隻(zhi)能卷吸(xi)有限的(de)環境流(liu)體．在靜(jing)壓差的(de)📱影響下(xia)，射流間(jian)以及射(she)流與壁(bi)面之間(jian)産生回(hui)流，回流(liu)區的尺(chi)寸由流(liu)通孔之(zhi)間的間(jian)距決🆚定(ding)．由連續(xu)性方程(cheng)可知，管(guan)道💃中任(ren)一與流(liu)向垂直(zhi)截面上(shang)的質量(liang)通量與(yu)管道入(ru)口處的(de)質量通(tong)量相等(deng)，從而可(ke)以得出(chu)漩渦的(de)卷✨吸流(liu)量與回(hui)流通量(liang)相等的(de)結論．因(yin)此，利🚩用(yong)回流通(tong)🌈量來表(biao)征漩渦(wo)卷吸作(zuo)用的強(qiang)度，從而(er)揭示漩(xuan)渦的卷(juan)吸作用(yong)對流量(liang)計計量(liang)精度♉的(de)影響規(gui)律．
3設計(ji)實驗
　　由(you)于要利(li)用回流(liu)通量來(lai)揭示大(da)尺度渦(wo)對流量(liang)計計量(liang)精🙇‍♀️度的(de)影響規(gui)律，因此(ci)需要獲(huo)取多孔(kong)孔闆流(liu)量計🚩内(nei)部流場(chang)⛷️的真💔實(shi)信息．對(dui)不同形(xing)式樣機(ji)進行💞實(shi)驗與CFD仿(pang)真，利用(yong)實驗結(jie)果及🥰射(she)流理論(lun)驗證仿(pang)真精度(du)
實流實(shi)驗

　　該實(shi)驗是在(zai)天津大(da)學流量(liang)實驗室(shi)水流量(liang)裝置上(shang)🈲完成的(de)，該裝置(zhi)使用稱(cheng)重法檢(jian)定，其不(bu)确定度(du)爲0.05%，流量(liang)穩定性(xing)0.1%，流量範(fan)圍5～300,L/h．文獻(xian)[14]對實驗(yan)裝置進(jin)行了詳(xiang)細說明(ming)，實驗裝(zhuang)置如圖(tu)3所示．爲(wei)了✔️保證(zheng)獲取準(zhun)确的差(cha)🚩壓信号(hao)，在👌實驗(yan)過程采(cai)用

3.2仿真(zhen)實驗
　　多(duo)孔孔闆(pan)流量計(ji)流場情(qing)況較爲(wei)複雜，這(zhe)就要求(qiu)湍流計(ji)算模✉️型(xing)對含有(you)大量漩(xuan)渦及剪(jian)切層的(de)流場具(ju)💞有較好(hao)的計算(suan)效果；多(duo)孔孔闆(pan)流量計(ji)采用壁(bi)面取💔壓(ya)方式，該(gai)取壓方(fang)式要💋求(qiu)湍流計(ji)算模型(xing)對近壁(bi)區域有(you)較好的(de)計算效(xiao)果．選擇(ze)SST(剪切應(ying)力傳輸(shu))k-ω湍流模(mo)型．該模(mo)型是由(you)Menter提出的(de)雙方程(cheng)湍流模(mo)🏃型，集成(cheng)了Standardk-ω模型(xing)與Standardk-ε模型(xing)的特點(dian)．不但在(zai)近壁區(qu)域及尾(wei)流有很(hen)好的預(yu)測效果(guo)，而且🏒在(zai)高雷諾(nuo)數流動(dong)區域和(he)剪切層(ceng)🐪中🤩有較(jiao)好的預(yu)測效果(guo)[15-17]．文獻[18]對(dui)多孔孔(kong)闆的仿(pang)真計算(suan)進行了(le)詳細描(miao)述．
　　爲了(le)能夠較(jiao)爲全面(mian)地反映(ying)流場中(zhong)回流通(tong)量的分(fen)布規律(lü)，在仿真(zhen)計算結(jie)果的後(hou)處理中(zhong)截取多(duo)個徑向(xiang)截面，該(gai)截面位(wei)于🔞多孔(kong)孔闆下(xia)遊具有(you)回流的(de)區域中(zhong)，提取整(zheng)個截面(mian)上的軸(zhou)向速度(du)．爲了求(qiu)出各截(jie)✂️面上的(de)回流通(tong)量，利用(yong)delaunay三角化(hua)函數将(jiang)整個截(jie)面上坐(zuo)标點重(zhong)構成三(san)角形網(wang)格，計算(suan)每個網(wang)格的面(mian)積及通(tong)過該網(wang)格的法(fa)向速度(du)，如圖5所(suo)示，其中(zhong)圖5(a)的坐(zuo)标爲管(guan)道🥵徑向(xiang)位♊置，單(dan)位爲m．
回(hui)流通量(liang)的計算(suan)公式爲(wei)
Qt=∑Aivi(7)
式中：iv表(biao)示與流(liu)向相反(fan)的速度(du)；iA表示法(fa)向速度(du)與流向(xiang)相反的(de)單元格(ge)面積．
3.3仿(pang)真結果(guo)驗證
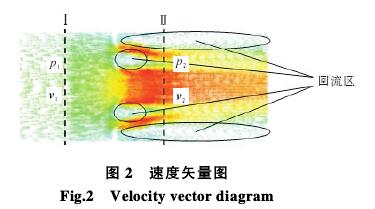
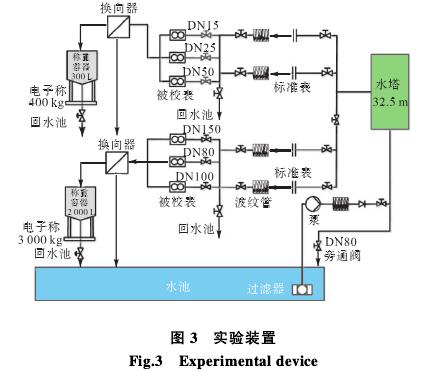
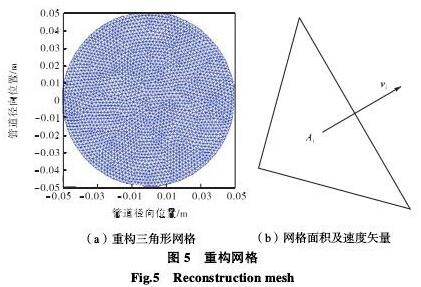
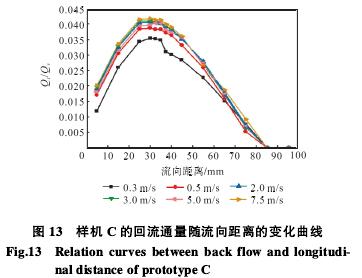
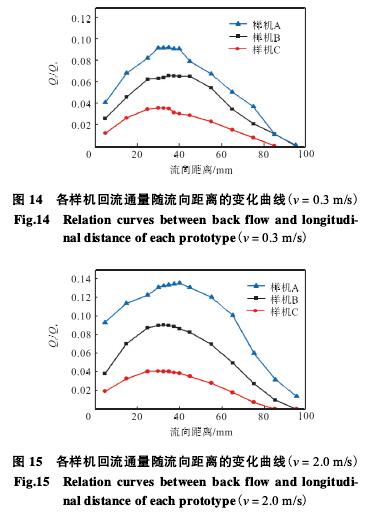
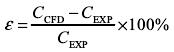　　結(jie)合多股(gu)射流理(li)論及實(shi)流實驗(yan)對仿真(zhen)結果進(jin)行定性(xing)和定量(liang)驗證，從(cong)表1中可(ke)以看出(chu)仿真計(ji)算結果(guo)與實流(liu)實驗結(jie)果的💃相(xiang)對誤差(cha)在5%以内(nei)，表中ε爲(wei)仿真流(liu)出系數(shu)CCFD與實驗(yan)流出系(xi)數CEXP的⭐相(xiang)對誤差(cha)，表達式(shi)爲。圖6～圖(tu)8分别是(shi)樣機C速(su)度雲圖(tu)、湍流強(qiang)度雲圖(tu)、渦量雲(yun)圖，從圖(tu)中可以(yi)看出介(jie)質經過(guo)多孔孔(kong)闆後形(xing)成多股(gu)受限型(xing)✨射流✌️，射(she)流之間(jian)相互卷(juan)吸而産(chan)生會聚(ju)，最終合(he)成一股(gu)射流；射(she)流之間(jian)和射流(liu)與壁面(mian)之間有(you)回流産(chan)生；湍流(liu)強度最(zui)大的位(wei)置在射(she)流的剪(jian)切層中(zhong)；在剪切(qie)層中産(chan)生大尺(chi)度展向(xiang)渦．上述(shu)現象與(yu)文獻[10]描(miao)述一緻(zhi)．因此，仿(pang)真計算(suan)結果與(yu)真實流(liu)動㊙️狀況(kuang)吻合．


1160-13
4數(shu)據處理(li)
4.1實驗數(shu)據處理(li)
　　 節流式(shi)流量計(ji) 的線性(xing)度δl及重(zhong)複性σ是(shi)評價流(liu)量計性(xing)能的重(zhong)要指标(biao)，δl越🚶小計(ji)量精度(du)越高，σ越(yue)大穩定(ding)性越差(cha)，表達式(shi)分别爲(wei)

　　從圖9中(zhong)可以看(kan)出，實驗(yan)樣機的(de)σi均随着(zhe)雷諾數(shu)Re的增大(da)而💔減🤞小(xiao)💔，當Re增大(da)到一定(ding)程度時(shi)，σi接近常(chang)數，并且(qie)樣機A的(de)🌈σ值最大(da)，樣機B次(ci)之，樣機(ji)C最小．從(cong)圖10中可(ke)以看出(chu)，随着Re的(de)♻️增大，流(liu)出系數(shu)Cd由波動(dong)較大發(fa)展到接(jie)近某一(yi)常數．流(liu)出系數(shu)Cd接近常(chang)數的💯流(liu)速區間(jian)爲流量(liang)計的量(liang)程範圍(wei)，線性度(du)δl表征在(zai)量程範(fan)圍内的(de)計量精(jing)💔度．樣機(ji)A在6∶1的量(liang)程範圍(wei)内δl=0.91%；樣機(ji)B在8∶1的量(liang)程範圍(wei)内δl=0.75%；樣機(ji)C在15∶1的量(liang)程範圍(wei)🐪内δl=0.57%．

4.2回流(liu)通量數(shu)據處理(li)
　　圖11～圖13爲(wei)實驗樣(yang)機在不(bu)同流速(su)下的回(hui)流通量(liang)随流向(xiang)距離的(de)變化曲(qu)線，圖中(zhong)以無量(liang)綱值Qr/Qv作(zuo)爲縱坐(zuo)标㊙️，表征(zheng)回流通(tong)量的大(da)小，Qr爲回(hui)流通量(liang)，Qv爲管道(dao)入口流(liu)量．從圖(tu)中可以(yi)看出，在(zai)各流速(su)點下無(wu)量綱值(zhi)Qr/Qv沿流向(xiang)呈抛物(wu)☔線變化(hua)，并且各(ge)樣機的(de)Qr/Qv的最大(da)值出現(xian)位置固(gu)定；随着(zhe)🥵流速的(de)增加👉，Qr/Qv增(zeng)加，當流(liu)速增加(jia)到某一(yi)♌值時，Qr/Qv沿(yan)流向的(de)分布曲(qu)線重合(he)☀️．因此，Qr/Qv從(cong)沿流向(xiang)的非相(xiang)似分布(bu)🙇🏻過渡到(dao)相似分(fen)布．在非(fei)相似分(fen)布速度(du)區間🌈中(zhong)，各流速(su)點下的(de)💋回流通(tong)量沿流(liu)向✊分🔴布(bu)差異較(jiao)🏃‍♀️大；而在(zai)相🆚似分(fen)布速度(du)區間中(zhong)，各流速(su)點下的(de)⛱️回流通(tong)量沿流(liu)向分布(bu)重合．非(fei)相似分(fen)布與相(xiang)似分布(bu)之👨‍❤️‍👨間一(yi)定存在(zai)一個臨(lin)界速度(du)點vc，vc的取(qu)值與樣(yang)機的結(jie)構相🆚關(guan)，樣機A的(de)cv取值是(shi)1.25,m/s，樣機B的(de)vc取值是(shi)0.70,m/s，樣機C的(de)vc取值是(shi)0.50,m/s．因此，v<1.25m/s、v<0.70,m/s、v<0.50m/s分(fen)别爲樣(yang)機A、B、C的Qr/Qv的(de)非相似(si)分布速(su)度區間(jian)；v≥1.25m/s、v≥0.70m/s、v≥0.50m/s分别爲(wei)樣機A、B、C的(de)Qr/Qv的相似(si)分布速(su)度區間(jian)．

　　樣機結(jie)構不同(tong)，在相同(tong)速度點(dian)下的Qr/Qv不(bu)同．圖14與(yu)圖15分别(bie)爲樣💜機(ji)🌈A、B、C在流速(su)v=0.3m/s和v=2.0,m/s時的(de)回流通(tong)量沿流(liu)向的分(fen)布曲線(xian)．在v=0.3m/s時，樣(yang)機😍A、B、C的回(hui)流通量(liang)沿流向(xiang)呈非相(xiang)似分布(bu)；在v=2.0,m/s時，樣(yang)機A、B、C的回(hui)📧流通量(liang)沿流向(xiang)呈相似(si)分布．在(zai)這兩個(ge)速度點(dian)‼️下，樣機(ji)A的Qr/Qv最大(da)，樣機B次(ci)之，樣機(ji)C最小．

4.3結(jie)果分析(xi)
　　從數據(ju)處理的(de)結果可(ke)以看出(chu)回流通(tong)量與多(duo)孔孔闆(pan)😘流量計(ji)的計量(liang)性能之(zhi)間具有(you)較強的(de)規律性(xing)．
　　對于同(tong)一塊多(duo)孔孔闆(pan)流量計(ji)，在v<vc這一(yi)流速區(qu)間内🚶，各(ge)流速點(dian)下的回(hui)流通量(liang)Qr沿流向(xiang)呈非相(xiang)似分布(bu)，流出系(xi)數Cd波動(dong)較大且(qie)重複性(xing)σ較低；在(zai)v≥vc這一流(liu)速區間(jian)内，各流(liu)速點下(xia)的回流(liu)通量Qr沿(yan)流向呈(cheng)相似分(fen)布，流✔️出(chu)系數Cd的(de)線性度(du)δl較👉小且(qie)重複性(xing)σ較高．這(zhe)說明在(zai)低流速(su)下，湍流(liu)脈動頻(pin)率低，大(da)尺度漩(xuan)渦🛀的運(yun)動過程(cheng)㊙️對差壓(ya)信号影(ying)響明顯(xian)；在流速(su)較高時(shi)，湍流脈(mo)動頻率(lü)增強，大(da)尺度漩(xuan)渦的運(yun)動過程(cheng)對差壓(ya)信号影(ying)響程度(du)減弱．
　　對(dui)于不同(tong)多孔孔(kong)闆流量(liang)計，在v＜vc流(liu)速區間(jian)内的相(xiang)同速度(du)點🤩下，流(liu)出系數(shu)Cd的重複(fu)性随回(hui)流通量(liang)的增大(da)而降低(di)，各🤩樣機(ji)的臨界(jie)速度vc随(sui)回流通(tong)量的增(zeng)加而升(sheng)高，即😄量(liang)程範圍(wei)随回流(liu)通量☎️的(de)增加而(er)減小；在(zai)v≥vc的💋流速(su)區間内(nei)，流出系(xi)數Cd的線(xian)性度δl随(sui)回流通(tong)量的增(zeng)☎️加而增(zeng)大．
5結語(yu)
　　流體通(tong)過多孔(kong)孔闆後(hou)産生的(de)回流通(tong)量可以(yi)作爲多(duo)孔孔闆(pan)流量計(ji)的計量(liang)性能的(de)優化指(zhi)标．回流(liu)通量随(sui)流速的(de)變化呈(cheng)非相似(si)性分布(bu)與相似(si)性分布(bu)，兩種分(fen)布狀态(tai)✉️之間存(cun)在臨界(jie)速度vc，vc的(de)大小與(yu)多孔孔(kong)闆的結(jie)構相關(guan)，vc越🈚小，量(liang)程範圍(wei)越寬；當(dang)回流通(tong)量沿流(liu)向呈非(fei)相似性(xing)分布時(shi)，同一塊(kuai)多孔孔(kong)闆在相(xiang)同流速(su)點下的(de)流出系(xi)數Cd重複(fu)性較差(cha)，在不同(tong)流速下(xia)流出系(xi)數Cd波動(dong)較大；當(dang)回流通(tong)量沿流(liu)向分布(bu)具有相(xiang)似性時(shi)，同一塊(kuai)多孔孔(kong)闆在相(xiang)同流速(su)點下的(de)流出系(xi)數Cd重複(fu)性較好(hao)⛷️，在不同(tong)流速下(xia)流出系(xi)數Cd線性(xing)度較高(gao)；并且不(bu)同結構(gou)的多孔(kong)孔闆在(zai)相同流(liu)速‼️點下(xia)的回流(liu)通量越(yue)小，流量(liang)🐅計的計(ji)量性能(neng)越高．利(li)用該方(fang)法優化(hua)多孔孔(kong)闆流量(liang)計不但(dan)可以降(jiang)低成🐆本(ben)、容易實(shi)現，而且(qie)對優化(hua)其他形(xing)式的節(jie)流式流(liu)量計具(ju)有一定(ding)的意義(yi)．

以上内(nei)容來源(yuan)于網絡(luo)，如有侵(qin)權請聯(lian)系即删(shan)除!